Eight Queens Problem
Tech Stack: GoogleColab, Python
What is the 8 queens problem?
The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other. In chess a queen can attack vertically, horizontally or diagnolly.
The image below shows a solution to the 8 queens problem.

How to solve this problem using a genetic algorithm?
To solve this problem I had to create a genetic algorithm(GA). A genetic algorithm is a search algorithm that imitates biology, specifically, mutation, crossover, fitness and selection.
Fitness
Fitness is a way to measure how "perfect" an indivdual is. In my GA the ideal individual or solution to the queens problem would be a fitness score of 0. My fitness score is measured by how many queens attack eachother on the board. For example on the board below. The 3rd row's ([0,1,2,3,4,5,6,7]) queen is getting attacked diagonally twice. Then each of those queens is also attacking once. Making the total fitness score 4.
The genomes of the individuals look like this [2 5 7 1 0 3 6 4] . They are represented by numbers 0-7 and each number can only be
used once. Each number represents the row the queen will be places in each coloumn. If the board were labeled 0-7 horizontally
and 0-7 vertically the top being 0 and bottom row being 7, then using the genome above:
- Column 0 will have a queen in row 2. [2]
- Column 1 will have a queen in row 5. [2 5]
- Column 2 will have a queen in row 7. [2 5 7]
- Column 3 will have a queen in row 1. [2 5 7 1]
- etc.
Each number represents the row it will be in the given column.
Setting up my genomes this way allows me to make sure each column and each row only has one queen. Attacks can only happen diagonally.
[2 5 7 1 0 3 6 4]
Queens Board
[0, 0, 0, 0, 1, 0, 0, 0]
[0, 0, 0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1]
[0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, 0]
[0, 0, 1, 0, 0, 0, 0, 0]
Fitness Score: 4
def fitness_score(self):
self.fitness = 0
for col in range(genomesize):
for row in range(genomesize):
if(row != col):
x = abs(col - row)
y = abs(self.genome[col] - self.genome[row])
if( x == y ):
self.fitness += 1
Selection
Selection in nature is how animals find a mate. Typically out of the options given the animal would choose the best mate. Whether it is by the color of their fur, their stregth or if they are good hunters. In order to simulate this in an algorithm and simulate the randomness of finding a good mate or not.
I choose 3 random individuals from the population and have them fight in a tournment gladiator style and may the best mate win.
The best fit individual would then have the chance to mate and create offspring and hopefully create better fit children.
def selection(population):
# array for 3 individual tourney
ind = []
tourney = 3
# add random individuals
for n in range(tourney):
ind.append(random.randint(0,pop_size - 1))
min = 101
# fine best fit in tourney
for n in range(tourney):
if ind[n] < min:
min = ind[n]
# index space where best fitness is
return population[min]
Crossover
Crossover in nature is the offspring. Think of the randomness of genes and how two different individuals
can have a child with a mixture of genes. That is essentially crossover. In my case I am imitating sharing genes in a
way that gets a random number 1-8 and swaps the genes. For example if 11111111 and 00000000 were to "mate" and have offspring.
My crossover algorithm will choose a random number 1-7, let's say it chose 3. The crossover point would be 111|11111 and 000|00000.Then after crossing over there will be two children 11100000 and 00011111. Since my genome has to be an array of 0,1,2,3,4,5,6,7. It is a bit tricky to make the crossover happen to not
have repeated numbers included which is why I used permutations. This will help solve the problem by making sure there is only one queen in each row by making sure there will be no
repeats.
def crossover(ind1, ind2):
# get random crossover point not including the end points
point = random.randint(1,6)
# copy parent genomes to crossover
p1 = ind1.genome
p2 = ind2.genome
# empy array to place new crossed over genes
c1 = []
c2 = []
# Copy over array before crossover point
for x in range(point):
if (x <= point):
c1.append(p1[x])
c2.append(p2[x])
# start index at x-over point
# check if not in the array and crossover
# cycle to begining to maintain permutation
while(len(c1) < len(p1) or len(c2) < len(p2)):
if p2[point] not in c1 and len(c1) < len(p1):
c1.append(p2[point])
if p1[point] not in c2 and len(c2) < len(p2):
c2.append(p1[point])
point += 1
point = point % 8
# create individuals as children
child1 = individual()
child2 = individual()
# make the genome equal new childrens
child1.genome = c1
child2.genome = c2
# return two children
return child1, child2
Mutation
Mutation is to create random genes or new genes. This helps simulate evolution. Like fish getting an extra fin to swim faster.
In this case the mutation happens to the individual itself so swapping two random numbers within its own genes.
def mutate(self):
a = random.randint(0,7)
b = random.randint(0,7)
# swap variables
temp = self.genome[a]
self.genome[a] = self.genome[b]
self.genome[b] = temp
Individual
Since this is a genetic algorithm we need "individuals" and genomes. In this case I created an individual class where individuals each have a genome, a fitness score and can mutate itself if needed.
class individual:
def __init__(self):
self.fitness = 0
self.genome = []
self.genome = np.random.permutation(8)
print(self.genome)
self.board = [[0 for i in range(genomesize)] for j in range(genomesize)]
self.print_board()
self.fitness_score()
def fitness_score(self):
self.fitness = 0
for col in range(genomesize):
for row in range(genomesize):
if(row != col):
x = abs(col - row)
y = abs(self.genome[col] - self.genome[row])
if( x == y ):
self.fitness += 1
print("Fitness Score: " + str(self.fitness))
def print_board(self):
print('\n' + "Queens Board")
# mark queens
for i in range(genomesize):
self.board[self.genome[i]][i] = 1
# print rows
for row in self.board:
print(row)
def mutate(self):
a = random.randint(0,7)
b = random.randint(0,7)
# swap variables
temp = self.genome[a]
self.genome[a] = self.genome[b]
self.genome[b] = temp
Survival
This is a function that keeps the population at 100. So if two new children are created then two individuals
have to die. Think of it as natural selection. My survival function finds parents with selection() and
uses those parents to get two children from crossover(). Eachchild is given a 20% chance to mutate and
before adding new children the two worst individuals in the population have to die.
def survival(population):
# find parents
p1 = selection(population)
p2 = selection(population)
# get children
c1 , c2 = crossover(p1,p2)
if random.random() < 0.2:
c1.mutate()
if random.random() < 0.2:
c2.mutate()
# removes worst 2 individuals from sorted population
population.pop()
population.pop()
# add children back to the population
population.append(c1)
population.append(c2)
return population
Solution:
Since this is a GA, a solution is not guaranteed. The code below shows me putting all the above functions and classes to use. I iterated the population 1000.
# initialize varibales
pop_size = 100
population = []
pop_iteration = 1000
bestFit = []
worstFit = []
aveFit = []
# initialize population
for i in range(pop_size):
population.append(individual())
# sort initial pop
population.sort(key=lambda x: x.fitness)
# iterate generationally
for i in range(pop_iteration):
population = survival(population)
population.sort(key=lambda x: x.fitness)
bestFit.append(population[0].fitness)
worstFit.append(population[pop_size - 1].fitness)
totalsum = 0
for x in range(pop_size):
totalsum += population[x].fitness
average = totalsum/pop_size
aveFit.append(average)
if i == 0:
print("initial Generation")
print(bestFit[i], worstFit[i], aveFit[i])
if i == pop_size - 1:
print("Final Generation")
print(bestFit[i], worstFit[i], aveFit[i])
Average Fit
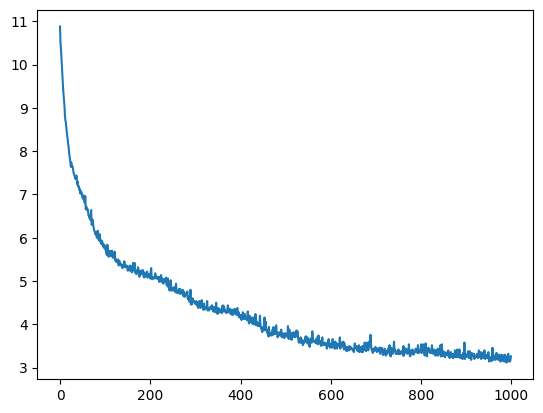
This does a great job of showing that the average fitness of the population is getting better after each generation.
Worst Fit
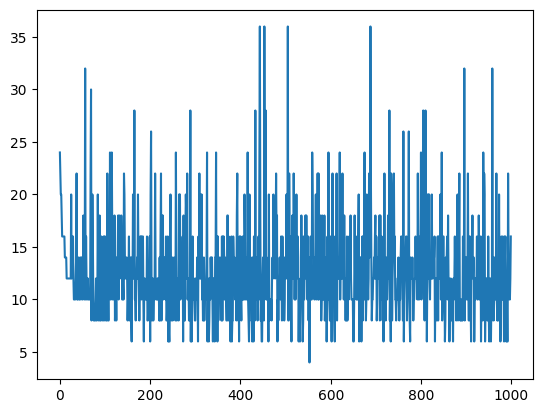
The worst individual in the population fluctuates alot. Which tells me my mutation function is probably at too high of a percentage because my new individuals (children) are sometimes really bad individuals.
Best Fit
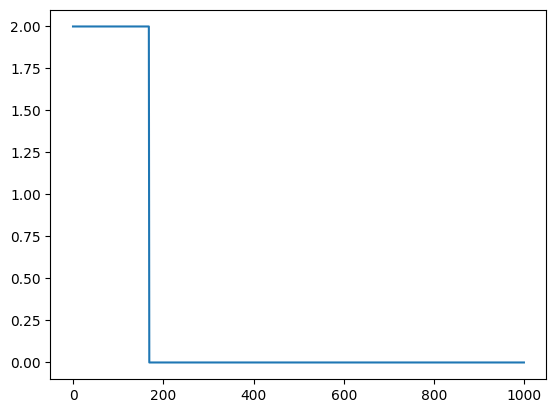
As you can see at about 180 iterations there is a solution that is found. On some runs the population does not find a solution at all. That is typical for genetic algorithms. They are search algorithms that do not guarantee a solution.